Probability Distributions

Probability distributions describe how the values of a random variable are distributed. They are fundamental to understanding the likelihood of different outcomes and form the basis for statistical analysis and inference in machine learning.

Discrete Distributions

Discrete probability distributions describe the probabilities of the possible values of a discrete random variable. A discrete random variable is one that has a countable number of possible values.

Binomial Distribution

The binomial distribution models the number of successes in a fixed number of independent Bernoulli trials, each with the same probability of success. It is defined by two parameters: \(n\) (number of trials) and \(p\) (probability of success).

The probability mass function (PMF) of a binomial random variable \(X\) is given by:

\[ P(X = k) = \binom{n}{k} p^k (1 - p)^{n - k} \]

where \(\binom{n}{k}\) is the binomial coefficient.

Poisson Distribution

The Poisson distribution models the number of events occurring in a fixed interval of time or space, given the average number of times the event occurs over that interval. It is defined by a single parameter: \(\lambda\) (average rate of occurrence).

The probability mass function (PMF) of a Poisson random variable \(X\) is given by:

\[ P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!} \]

Continuous Distributions

Continuous probability distributions describe the probabilities of the possible values of a continuous random variable. A continuous random variable is one that has an infinite number of possible values.

Normal (Gaussian) Distribution

The normal distribution, also known as the Gaussian distribution, is one of the most important continuous distributions in statistics. It is defined by two parameters: \(\mu\) (mean) and \(\sigma\) (standard deviation).

The probability density function (PDF) of a normal random variable \(X\) is given by:

\[ f(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} e^{-\frac{(x - \mu)^2}{2 \sigma^2}} \]

Exponential Distribution

The exponential distribution models the time between events in a Poisson process. It is defined by a single parameter: \(\lambda\) (rate parameter).

The probability density function (PDF) of an exponential random variable \(X\) is given by:

\[ f(x) = \lambda e^{-\lambda x} \]

for \(x \geq 0\).

Applications in Machine Learning

Probability distributions are extensively used in machine learning for various purposes, including:

• Modeling Uncertainty: Probability distributions are used to model the uncertainty in data and predictions.

• Parameter Estimation: Many machine learning algorithms involve estimating the parameters of underlying probability distributions.

• Hypothesis Testing: Probability distributions are used to perform hypothesis tests and make inferences about population parameters.

• Bayesian Inference: Probability distributions are central to Bayesian methods, where prior distributions are updated with data to obtain posterior distributions.

Examples of Probability Distributions in Python

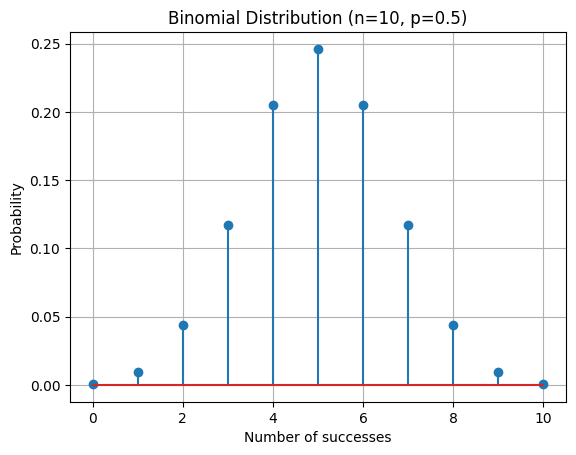
Binomial Distribution Example

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom

# Parameters
n = 10  # Number of trials
p = 0.5  # Probability of success

# Binomial distribution
x = np.arange(0, n + 1)
pmf = binom.pmf(x, n, p)

# Plot
plt.stem(x, pmf)
plt.xlabel("Number of successes")
plt.ylabel("Probability")
plt.title("Binomial Distribution (n=10, p=0.5)")
plt.grid()
plt.show()

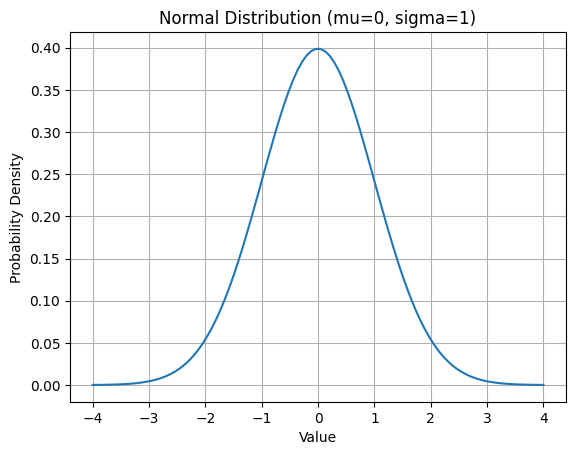
Normal Distribution Example

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# Parameters
mu = 0  # Mean
sigma = 1  # Standard deviation

# Normal distribution
x = np.linspace(mu - 4 * sigma, mu + 4 * sigma, 100)
pdf = norm.pdf(x, mu, sigma)

# Plot
plt.plot(x, pdf)
plt.xlabel("Value")
plt.ylabel("Probability Density")
plt.title("Normal Distribution (mu=0, sigma=1)")
plt.grid()
plt.show()

Summary

Probability distributions are a cornerstone of statistical analysis and machine learning. They provide a mathematical framework for understanding the likelihood of different outcomes and modeling uncertainty. By mastering probability distributions, you can better analyze data, make inferences, and build robust predictive models.

In the next section, we will delve deeper into Bayes’ Theorem, which is fundamental for updating probabilities based on new evidence.